目次
はじめに
抜き打ちテストのパラドックスは、思考実験やパラドックスの一種であり、確率や予測の限界について考える上で興味深い事例です。
本記事では、抜き打ちテストのパラドックスの概要やその背後にある論理を解説し、さらに、このパラドックスが持つ意味や、それが私たちの日常生活や意思決定に与えるインパクトについても考察していきます。
抜き打ちテストのパラドックスとは
抜き打ちテストのパラドックスとは、抜き打ちテストをいつ行われるのか全く予想ができないものと仮定すると、抜き打ちテストは不可能であるとの結論に行きつくという逆説です。
学校の先生が、抜き打ちテストを翌週の月曜から金曜のいずれか1日に行うと宣言したとします。
抜き打ちテストは、テストがいつ行われるかわからないものであるとの前提のもと、テストの実施日を予想します。
まず、金曜日にテストがあると仮定すると、月曜から木曜にテストがないことから、木曜日の夜には金曜が抜き打ちテストの日だと予想されてしまうので、金曜日はあり得ません。
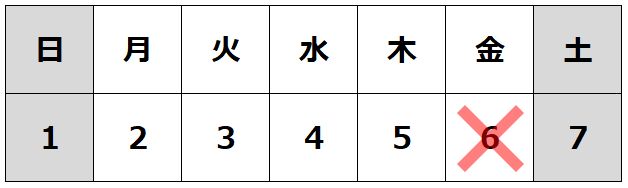
次に、木曜日にテストがあると仮定すると、同様に水曜日までテストがないことから、水曜の夜の時点で木曜か金曜がテストの日だと予想されてしまいます。
そして、先ほどの議論から金曜はあり得ないので、木曜だと予想されてしまいます。
よって木曜もあり得なくなります。
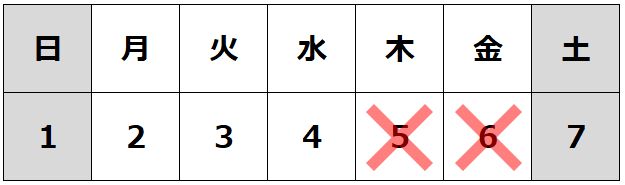
同様の手順で推理をしていくと、水曜、火曜、月曜にも抜き打ちテストができなくなってしまうのです。
よって、全ての曜日で抜き打ちテストが行われることはないという結論になります。
しかし、その一方で、全ての曜日の可能性が消えることで、逆にどの曜日にテストが行われるかわからなくなってしまうという逆説が発生するのです。
抜き打ちテストのパラドックスの背後にある論理
抜き打ちテストのパラドックスは、予測の限界や確率に関する興味深い問題を提起しています。
このパラドックスが示すのは、未来の事象に関する予測が、必ずしも正確ではないこと、そして、その予測が矛盾することがあるという事実です。
このパラドックスを通じて、私たちは予測や意思決定の難しさ、および、それらがもたらす不確実性について考えることができます。
抜き打ちテストのパラドックスの意味
抜き打ちテストのパラドックスは、現実世界においても、予測が難しい事象や状況に遭遇することがあることを示しています。
例えば、株価や経済の動向、自然災害の発生などは、予測が困難であり、矛盾する予測が生じることがあります。
このような状況下では、私たちはどのようにして最善の選択を行い、リスクを最小限に抑えることができるのでしょうか。
抜き打ちテストのパラドックスと意思決定
抜き打ちテストのパラドックスが教えてくれるのは、未来の予測が困難であることを受け入れ、それを考慮に入れた意思決定を行うことの重要性です。
具体的には、以下のような方法が考えられます。
- 複数のシナリオを想定する: 未来の予測が困難である場合、複数のシナリオを想定し、それぞれのシナリオに対して最善の選択を行うことが有効です。
- リスクの分散: 一つの選択肢に固執せず、リスクを分散させることで、不確実性を最小限に抑えることができます。
- 柔軟な対応: 予測が困難であることを認識し、状況が変化した場合に素早く対応できるように、柔軟な考え方や行動が求められます。
全曜日楽チンの法則
抜き打ちテストのパラドックスを応用すれば、つらい平日も楽な気分で切り抜けることができます。
普通の社会人にとっては、土曜日と日曜日が楽しみで、月曜日から金曜日は嫌な仕事の日という扱いでしょう。
しかし、翌日が楽しい土曜日である金曜日は、良い気分で仕事ができるという人が多いと思います。
つまり、仕事の日でも、翌日が良い日であれば、その日も良い日であると考えることができるのです。
よって、翌日が土曜日の金曜日は良い日だということになります。
この考えを続けていけば、良い日である金曜日の前日の木曜日も良い日ということになり、その木曜日の前日である水曜日も良い日だということになります。
こうした考えは月曜日まで続けることができ、全ての曜日が良い日だということになるのです。
まとめ
抜き打ちテストのパラドックスは、未来の予測や確率に関する興味深い問題を提起しており、その背後にある論理を理解することで、私たちの日常生活や意思決定においても有益な示唆を得ることができます。
このパラドックスから学ぶべきは、未来の予測が困難であることを受け入れ、それに対応するための柔軟な思考や行動が重要であるということです。
また、抜き打ちテストのパラドックスは、教育やビジネスなど様々な分野で活用されることがあります。
例えば、企業は環境変化に対応するために、複数のシナリオを想定し、リスク分散や柔軟な経営戦略を立てることが求められます。
教育現場でも、抜き打ちテストを通じて、生徒たちが自主的に学習し、未来の不確実性に対処できるような能力を養うことが重要です。
さらに、抜き打ちテストのパラドックスは、倫理や哲学の問題としても考察されることがあります。
例えば、予測が困難であることを前提とした場合、私たちはどのような基準で道徳的な判断を下すべきなのか、あるいは、社会全体が抱えるリスクに対して、どのように責任を分担すべきなのかといった問いが浮かび上がります。
最後に、抜き打ちテストのパラドックスを理解することで、私たちは予測や意思決定の難しさを認識し、より適切な判断や行動ができるようになることが期待されます。
未来は不確実であり、予測が完全に正確であることはあり得ませんが、抜き打ちテストのパラドックスを参考に、複数のシナリオを想定し、リスクを分散させ、柔軟に対応することで、不確実な未来に立ち向かう力を身につけることができるでしょう。
本サイトで紹介している用語一覧は以下です。


木曜日にテストを設定した場合、水曜日の夜の時点で「明日テストがある」と
予想されてしまうと思います。
なぜなら金曜日にはテストができないためです。
実際に金曜日にテストを設定した場合、木曜日の夜の時点で「明日テストがある」と
予想されてしまい、教師のルール違反となり、金曜日にはテストができません。