ここでは、日常会話で使える知的な小話と、実際の使用例を紹介します。
サンクトペテルブルクのパラドックスとは
サンクトペテルブルクのパラドックスとは、期待値計算に基づく意思決定の際に発生する逆説で、 極めて少ない確率で極めて大きな利益が得られるような場合に、期待値が発散し、 誤った結論にたどり着くというものです。
例えば、裏が出るまでコインを投げ続け、表が出た回数が1回なら1円を獲得、2回なら2円を獲得、3回なら4円を獲得というように、表が連続で出れば出るほど倍の金額が貰えるゲームを想定します。
あなたなら、このゲームの参加費がいくらなら参加したいと思いますか?
こうしたギャンブルに参加すべきかどうかは、期待値を計算すればわかります。
期待値とは、そのギャンブルに参加した場合に得られる平均リターンです。
例えば、サイコロを1回投げて、その目の金額が貰えるゲームがあるとすれば、そのゲームの期待値は3.5です。

つまり、サイコロのゲームの参加費が、期待値より低い金額(=3.5円未満)であれば、参加した方が良いということになります。
話を戻して、コインを投げて連続で出た表の枚数に応じて倍々の金額が貰えるゲームの期待値を考えてみます。
期待値を求めるためには、起こりうる全ての値を合計し、それぞれ確率で除算する必要があります。
ここで、コインの表の回数ごとの貰える金額とその確率を表に整理してみます。
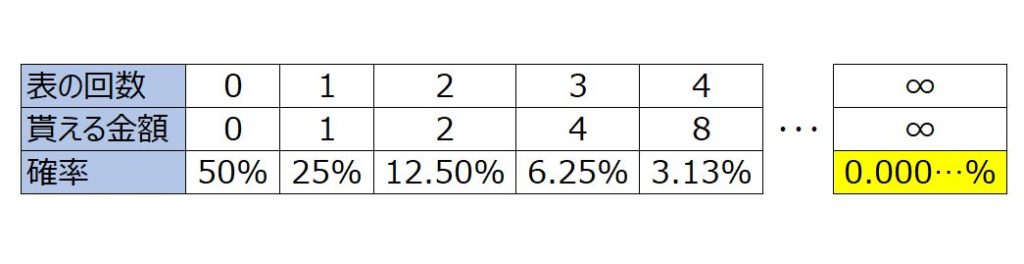
理論上、裏が一度も出ずに、表が無限に続く場合もありますので、ごくわずかな確率ですが、無限の金額が貰える場合もあります。
無限をどんな数字で割っても無限のままなので、このゲームの期待値も無限だということになります。
そのため、期待値だけを考えると、このゲームの参加費がどれだけ高くても参加すべきだということになります。
実際には表が無限に続くことはあり得ないので、期待値的には正しくともこの結論は間違いだという点で、パラドックスが発生していると言えます。
ギャンブルと期待値の関係については、以下の記事で詳しく紹介していますので、興味のある方は見てみてください。
現実的な回答は?
このように、ごく小さな単位を考慮することで誤謬が発生するという点で、サンクトペテルブルクのパラドックスはゼノンのパラドックスの亜種だとも言えます。
ゼノンのパラドックスは、俊足の青年が前方にいるのろまな亀を永遠に抜かせないとするアキレスと亀の話に代表されるような逆説です。
あまりに小さい単位の事象を考慮しても、正しい結論は導き出せません。
コインが連続で27回出ると賞金が1億円を超えるので、そこを現実的な最大値だと考えて計算すると、期待値は約14円となります。
もしあなたがこのゲームに参加するか聞かれた場合は、参加費が13円程度であれば参加してもよいでしょう。
日常会話での使用方法
「コイントスゲームしようぜ!」
「やだ」
本サイトで紹介している用語一覧は以下です。

