ここでは、日常会話で使える知的な小話と、実際の使用例を紹介します。
ラッセルのパラドックスとは
ラッセルのパラドックスとは、自身を要素として含まない、集合全体の集合を仮定した時に生じる矛盾のことです。
例えば、A以外の全てのアルファベットを含む集合を「A」と定義した時、集合としての「A」自身を、集合としての「A」に含めるべきかという問題が生じます。
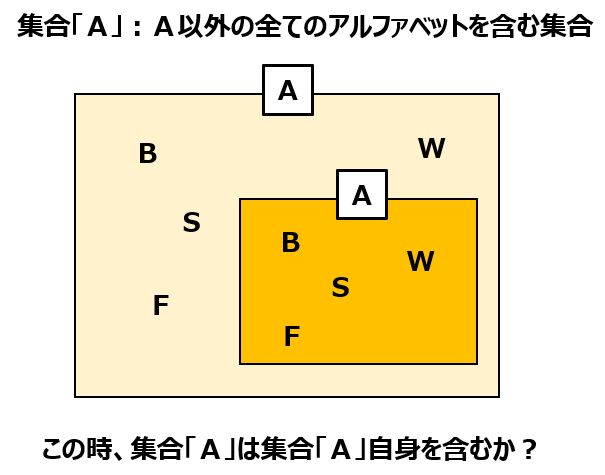
集合としての「A」自身を、集合としての「A」に含める場合、集合としての「A」の定義である「Aを含まない」に違反してしまいます。
一方で、集合としての「A」自身を、集合としての「A」に含めない場合も、「A以外の全てのアルファベットを含む」という集合としての「A」の定義に違反します。
結果として、どちらに捉えても最初に定義したルールに違反するため、矛盾が発生するのです。
抽象的でわかりづらいので、簡単な例を挙げて考えてみましょう。
不在市長のパラドックス

自分が市長をしている市に住んでいない市長を「不在市長」と呼ぶことにします。
不在市長が集まってひとつの市「不在市長市」を作ることになりました。
その市には不在市長だけが住んでおり、全ての不在市長が住みます。
このとき、不在市長市の市長Aは、どこにも住むことができなくなっていまいます。
市長Aが不在市長市に住むと、市長Aは自らが市長をしている市に住むため不在市長ではなくなり、「不在市長市は不在市長のみが住む」というルールに矛盾します。
また、市長Aが不在市長市以外の市に住むと、市長Aは自らが市長をしている市には住んでないため、不在市長となりますが、「不在市長市にはすべての不在市長が住む」というルールに矛盾してしまいます。
よって、 不在市長のみが住む不在市長市は定義不可能であることがわかります。
理髪師のパラドックス

別の例としては、理髪師のパラドックスがあります。
ある村でたった一人だけ理髪師がいるとします。
その理髪師は、自分で髪を切らない人全員の髪を切り、それ以外の人の髪は切りません。
この時、理髪師自身の髪は誰が切るのかを考えると、矛盾が生じます。
理髪師が自分の髪を切らないとするならば、理髪師は自分で髪を切らない人となり、「自分で髪を切らない人全員の髪を切る」というルールに反します。
また、理髪師が自分の髪を切るとするならば、「理髪師は自分で髪を切る人の髪は切らない」というルールに違反します。
よって、「自分で髪を切らない人全員の髪を切り、それ以外の人の髪は切らない」という定義自体が成立しないことがわかります。
集合に関しての興味深い話として、カラスを1羽も調べることなく、全てのカラスが黒いことを証明可能であるとする、ヘンペルのカラスも有名です。
日常会話での使用方法
「不在市長を集めて不在市長市を作ると・・・」
「何のためにそんなことすんの?」
本サイトで紹介している用語一覧は以下です。

