ここでは、日常会話で使える知的な小話と、実際の使用例を紹介します。
必要条件とは
2つの条件「P」と「Q」について、「PならばQ」が成り立つ時、QはPの必要条件であると言います。
「リンゴならば果物である」という命題を考えてみます。
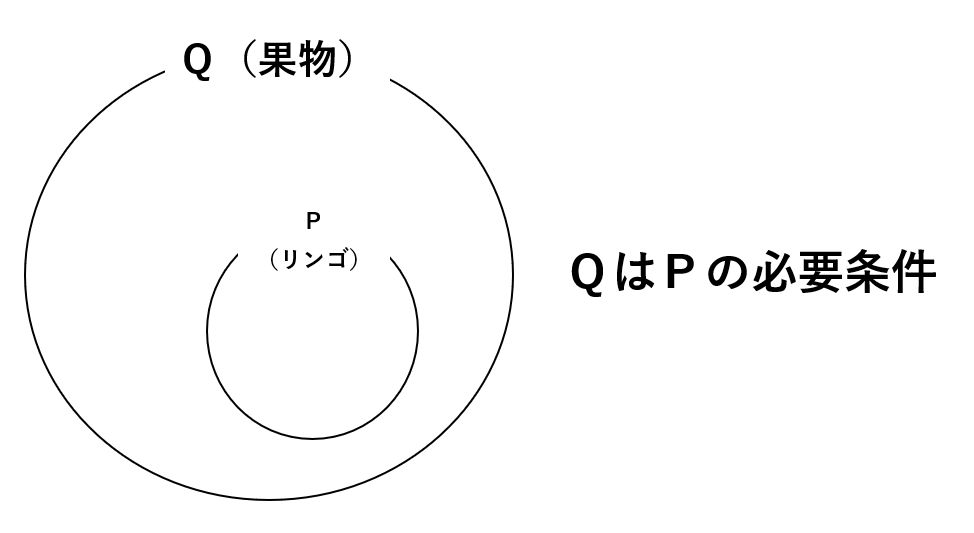
リンゴは果物なので、「PならばQ」という条件に当てはまっており、果物であることはリンゴであることの必要条件だと言えます。
リンゴであるという条件を満たすためには、そもそも果物である必要があるため、Q(=果物であること)はP(=リンゴであること)の必要条件だということになります。
十分条件とは
2つの条件「P」と「Q」について、「PならばQ」が成り立つ時、PはQの十分条件であると言います。
再び「リンゴならば果物である」という命題を考えてみます。

当然、リンゴは果物なので、「PならばQ」という条件に当てはまっており、リンゴであることは果物であることの十分条件だと言えます。
リンゴである時点で果物であることを十分に保証するため、P(=リンゴであること)はQ(=果物であること)の十分条件だということになります。
必要十分条件とは
2つの条件「P」と「Q」について、「PならばQ」と「QならばP」が同時に成り立つ時、PはQの必要十分条件であると言います。
逆の場合も同様なので、QもPの必要十分条件だと言えます。
あまり意味の無い文章ですが、「リンゴはリンゴである」という命題を考えてみます。
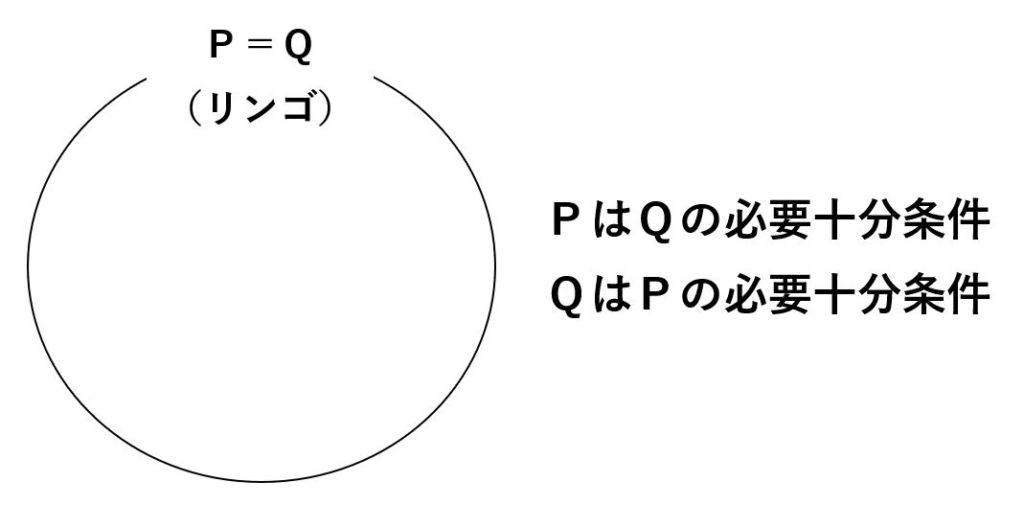
当然、リンゴがリンゴであることに間違いは無いため、「PならばQ」と「QならばP」が同時に成り立ち、リンゴであることはリンゴであることの必要十分条件だと言えます。
必要十分条件であるということは、「P」と「Q」はイコールの関係にあるということになります。
例題
以下のPはQのそれぞれ必要条件、十分条件、必要十分条件のどれでしょうか。
問①
P:4の倍数である
Q:偶数である
⇒ QはPの「???」条件である
問②
P: x=1
Q: x2=1
⇒ PはQの「???」条件である
問③
P: x3=8
Q: x=2
⇒ PはQの「???」条件である
少し考えてみてください。
答えは下の方に記載してあります。
・・・
・・・
・・・
・・・
・・・
・・・
・・・
・・・
・・・
・・・
・・・
・・・
問①
P:4の倍数である
Q:偶数である
⇒ QはPの「???」条件である
答えは「QはPの必要条件である」です。
偶数の定義は2で割り切れる整数なので、4の倍数であれば必ず偶数になります。
よって「PならばQ」が成り立つため、QはPの必要条件だと言えます。
逆に、偶数であったとしても、必ずしも4の倍数ではない(例えば2や6)ため、必要十分条件ではありません。
問②
P: x=1
Q: x2=1
⇒ PはQの「???」条件である
答えは「PはQの十分条件である」です。
Qの「x」に「1」を代入すると、「12=1」が成立することから、「PならばQ」が成り立つため、PはQの十分条件だと言えます。
逆に、「x2=1」の解としては「±1」であり、必ずしも「x=1」は成り立たないため、必要十分条件ではありません。
問③
P: x3=8
Q: x=2
⇒ PはQの「???」条件である
答えは「PはQの必要十分条件である」です。
Pの方程式を解くと、「x=2」というのが唯一の解となります。
よって、PとQは同値であり、「PならばQ」も「QならばP」も同時に成り立ちます。
日常会話での使用方法
「僕であることはイケメンであることの十分条件だ」
「なんだこいつ」
本サイトで紹介している用語一覧は以下です。

