ここでは、日常会話で使える知的な小話と、実際の使用例を紹介します。
大数の法則とは
大数の法則とは、試行回数やサンプルの数が多くなれば、事象の結果は計算上の確率に近づくという確率論や統計学における原理の1つです。
例えば、コイントスをして表が出る確率と、裏が出る確率はそれぞれ50%ですが、コインを10回投げただけでは、表が7回で裏が3回(表が70%で裏が30%)のように、バラつきが生まれることもあるでしょう。
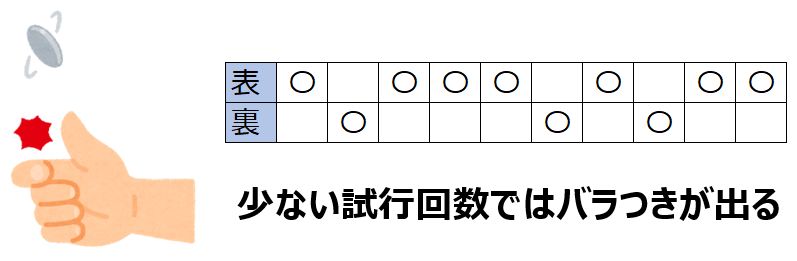
一方で、コイントスの試行回数を限りなく増やしていくと、回数が増えるにつれて、表と裏の結果はどちらも理論上の確率である50%に近づいていきます。
こうした性質から、世論調査や視聴率などの統計を取る際は、サンプルの数が多ければ多いほど、結果が信頼できるということになります。
しかし、サンプルの数が一定程度に大きくなると、それ以上サンプルを増やしても確率の信頼性の伸びはさほど大きくなくなるので、ある程度の母数を調査した時点で信頼できる統計とみなす方法が一般的です。
ギャンブラー必殺の法則
パチンコ店が利益を上げることができるのも、大数の法則のおかげです。
例えば、10万円分遊ぶと平均して8万円分のパチンコ玉を返すような還元率が80%のパチンコ台を店に置くことを考えます。
還元率は理論的な期待値なので、このパチンコ台を1台だけお店においていても、運が悪ければ(客にとっては運が良ければ)当たりが理論値を超えて発生し、パチンコ店が損をすることもあるでしょう。
しかし、このパチンコ台を100台おいておけば、大数の法則により確率は収束し、トータルでの還元率は80%に近づくため、店側は理論値通りの回収率で利益を得ることができるでしょう。

多くの試行回数を確保すること(ここでは多くのパチンコ台を用意すること)で、たまたま当たりが連続で発生した台があっても、全然当たりが出ない台も同時に生まれることため、バランスを取ることができるのです。
モンテカルロ法
大数の法則を利用して円周率を求める有名な方法として、モンテカルロ法があります。
モンテカルロ法では、1辺が1cmの正方形を用意し、その中のランダムな位置に点を大量に打ちます。
そして、その点が左下の原点から1cmの範囲内(下図の青い範囲)に入った個数を数えます。
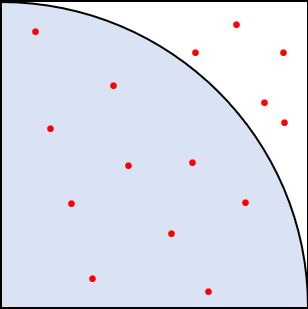
正方形の一辺の長さは1cmであることから、正方形の面積は「1」cm²(1辺×1辺)であり、図の青い扇形の面積は「π/4」cm²(半径×半径×π÷4)となります。
ここで、打った全ての点の数をNとし、扇形の範囲内に入った点の数をXとすると、扇形の範囲内に入る点の確率である「X/N」は「π/4」とイコールであることになります。
そしてその式を変形することで「π」と「4X/N」がイコールとなり、ランダムに配置した点の分布から、円周率の近似値が求められることになります。
正方形の中に点を大量に打つだけで、円周率の近似値が大数の法則から導き出せるのです。
日常会話での使用方法
「確率は収束するからこのパチンコで勝てるはずだ!」
「自分が負ける方に収束するんだぞ・・・」
本サイトで紹介している用語一覧は以下です。

